Knitting, algebra, & the promise of proficiencies

What could it look like to get credit for real world math proficiency?

Here’s something you should know about me: I knit furiously.

All the women in my family do. I learned to knit when I was six, lovingly coached by my grandmother, my mother, and my great aunt, a magician who could turn anything into a child-size sweater. And now, mumblety-three years later, I design and make my own knitting patterns. I hack existing patterns for size and gauge. And I spin my own yarn.

Here’s something else you should know about me: I failed algebra II. Twice.

But maybe I shouldn’t have.

Knitting means algebra

Knitting takes a lot of math. Let me give you an example.

Yarn substitutions require ratios & equations

Those lovely lovely patterns you see in glossy magazines and on ravelry have been worked up with a very particular yarn in mind. One specific yarn. Likely one the magazine is selling ads for. Now, like many knitters, I buy yarns based on color, price, lack of mohair (don’t get me started), softness, and availability at my local yarn shop. But when you substitute a different yarn, you have to translate gauge. Gauge, in knitting, is how many rows and how many columns make up a four inch square of knitted fabric.

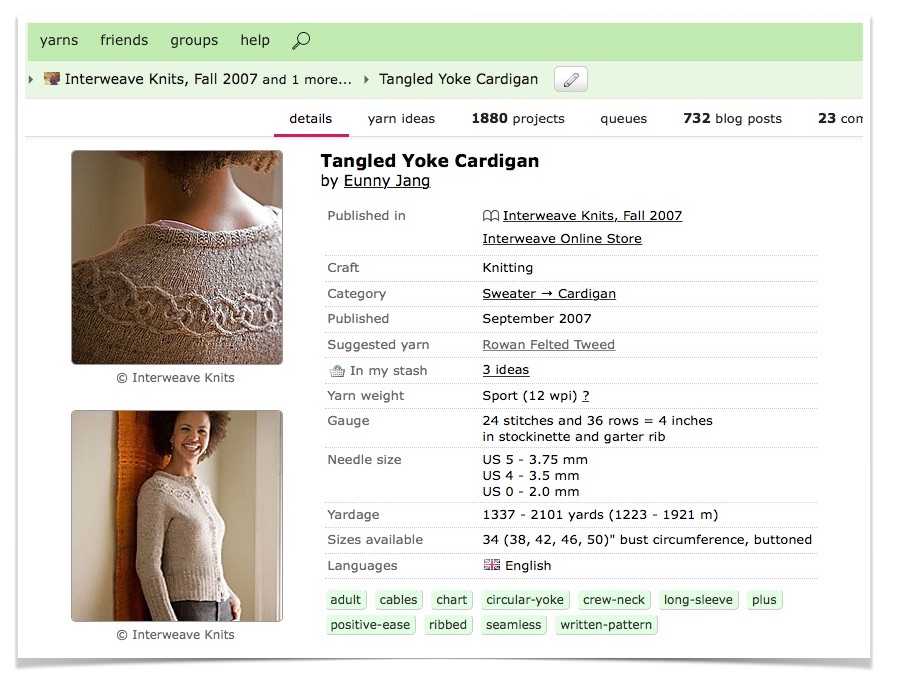
So, here’s a pattern listing for Eunny Jang’s Tangled Yoke Cardigan:

Jang designed the pattern for Rowan Felted Tweed yarn; to make this sweater along the sizes she’s outlined, you need to make sure your knitting hits 24 stitches and 36 rows. Otherwise all the instructions in the pattern will be wrong; 24 stitches in sport-weight yarn take up a very different amount of space than 24 stitches in bulky yarn, and 24 stitches in lace yarn.

I used Harrisville Designs Shetland (in colorway “Zinnia”, thanks for asking), which is a fingering weight yarn. Shetland has a gauge of 26 stitches and 26 rows. 24 divided by 26 is 0.92; my substituted yarn produces knitting that is 8% wider than the original.

Ditto for the rows. 26 divided by 36 equals 0.72; my yarn produces knitting that’s a whopping 28% shorter than the original called for in the pattern.

But with those two numbers in hand, I know how to translate the measurements in Jang’s pattern so that my cardigan fits well.

*Extreme Tim Gunn voice* “Make it work!”

For argument’s sake, let’s say I made the size with the 34″ bust circumference. Jang’s instructions state, “With largest needles, CO [cast on] 202… sts.” But! Knowing I need to account for my yarn giving an 8% of extra width, I cast on instead: 202 stitches * .92, or 186 stitches.

I also know when buying my yarn that I’ll need, not the 1337 yards called for in the original pattern, but 1337 yards plus 28% for length and minus 8% for width, and an extra 10% to ensure I don’t run out. (1734 yards total).

And so on.

That’s just one example of knitting and algebra. You also use math to solve questions like:

• How many 153-yard skeins do I need to knit a pullover that totals 2130 yards?
• If I need to increase 6 stitches evenly across a 202-stitch row, how many stitches should be between each increase?
• Now I’ve designed a cardigan/pullover/tank based on actual body measurements, how do I ensure it has 1 inch of positive ease? 2 inches?
• Given my gauge of n stitches per inch and a total length of 18 inches, how many stitches do I need to pick up for a buttonband running all the way along the front of my cardigan?

These things do not match up

Now, I can do these types of equations on the fly. They make sense to me intuitively. I can picture the garment in my head and the little math bees that live in my brain (go with it) buzz happily around and around the piece in question. They understand what needs shrinking, and what needs lengthening. All the bits that will make a garment fit correctly.

But again: I failed algebra II twice.

On paper, I could not meet the standards of the course, while at the same time I was deeply proficient in math in real world applications.

I grew up in a deeply rural area of Central California, in a ranching town. Nearly everyone I knew had sheep, goats or horses. I mucked stalls, I helped friends shear their sheep and pushed hay bales with all my might. I knit all the time, and had tiny notebooks filled with drawings of tanks (so many tanks, y’all) after having blown my allowance at the local Michael’s. Probably on terrible eyelash yarn, but still.

In Vermont, we have Act 77 and proficiency-based education. And I’m wondering how students who have these out-of-school passions, who are truly good at something outside the classroom, can get credit for that knowledge. How can personal passions that require math, engineering, economics, more math, anatomy, and project management skills enter the classroom and the student PLP portfolio in a meaningful way?

We know students do much more than knitting and algebra outside the classroom. We know there are students who raise goats and sheep and younger siblings. Some of them plan meals and budget groceries. Some of them build websites and businesses, and code games and write musicals.

Let’s start with the PLP

Thinking about the options available to us via Act 77, the PLP most readily springs to mind. I could have documented all the math I was doing as part of my PLP. The knitting site Ravelry functions as a digital portfolio site for knitters. You post photos of your projects, explain which yarns and needles you used, and document any modifications, like I did above.

A page on a student’s PLP showing their knitting (or goats, or sheep, or younger siblings, or websites) is a good start. But it goes hand-in-hand with having the expectation of some form of reflection (which we love to talk about here on our blog), and some form of documentation.

The question then becomes: how do you evaluate something like that?

Seek out the knowers in your community

It’s not realistic to expect that all educators can tell, at a glance, whether you’ve calculated your positive ease correctly. But there are very likely people in your community with that specific skillset. Local yarn shops are nexus points for people who have knit since time began, and most of them absolutely love to provide feedback. Think your buttonband’s wonky? Wonder whether your sleeve’s set in correctly? Head to the local yarn shop.

Most local yarn shops adore the feedback process so much they offer classes as well as hosting drop-in knitting hours. What would it look like to approach one of those yarn shops and ask if anyone there would be interested in providing a formal assessment? Or serving as a partner in a learner’s journey to publish their first book of patterns (or litter of goats, Scratch game, cookbook etc).

And that’s just a first step. If you sit down with your teaching team or administrators, how can you see proficiencies finding a way to capture out-of-school learning that encompasses real world skills?

Read more about knitting and algebra

For a fascinating deep dive:

• How Much Yarn Do I Need? A Mathematical Approach (.pdf)
• The Stunning Symbiosis Between Math and Knitting
• The algebra of knitting
• Who Knew Math and Knitting Were So Closely Knit?
• Knitting is Coding and Yarn is Programmable
• Can Learning to Knit Help Learning to Code?